CM2/6e
Algorithmique et logique
Géométrie
Grandeurs et mesures
Nombres et Calculs
Organisation et gestion de données, fonctions
Lors d’un voyage en Chine, Marco a trouvé dans le manuscrit Chu Chang Suan Shu un puzzle représentant un cercle inscrit dans un triangle.
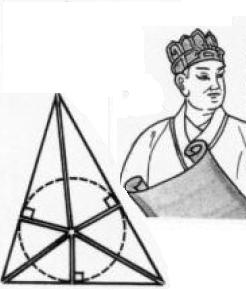
Dans ce triangle sont tracés les segments joignant les sommets au centre du cercle ainsi que les rayons du cercle aux points de contact avec les côtés du triangle.
En découpant ce triangle selon les segments tracés, on obtient 6 pièces triangulaires.
Ce puzzle permet de démontrer la formule R = 2S/P,
où S désigne l’aire du triangle, P son périmètre et R le rayon du cercle inscrit.
Tracer un triangle de côtés 10, 12 et 14 cm avec son cercle inscrit et ses 3 rayons caractéristiques.
Agencer ces 6 pièces en une bande rectangulaire de largeur R , puis expliquer comment on obtient alors la formule énoncée ci-dessus.
Mots-clés : Niveau 2de , épreuve de Mars 2002 , exercice 11.
Principaux éléments mathématiques : Cercle inscrit dans un triangle, bissectrices, tangent, rectangle, aire.
Capacités : Effectuer des tracés au compas, à l’équerre, Utiliser les théorèmes de la géométrie plane
Ce que l’élève doit faire : Tracer le cercle inscrit d’un triangle, découpage, puzzle, déduction, raisonnement logique.
Difficulté : **.
solution (exercice 11).