Partage arboré

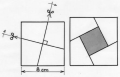
Donner deux partages possibles de ce terrain en huit parcelles en respectant les contraintes suivantes :
• • les huit parcelles doivent avoir la même forme ;
• • chaque parcelle doit contenir un des cercles représentés.

EGALIT’AIR

Démontrer que les deux domaines grisés ont des aires égales.

Sans Pi, tant pis

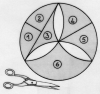
La rosace ci-contre est construite à partir d’un hexagone régulier. Avec les six pièces indiquées, on peut composer un rectangle. Calculer l’aire de la surface grisée.

A la baguette

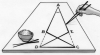
Sur la figure ci-contre, les points A, B et D sont alignés ainsi que les points A, E et C.
AE = ED = DC = CB = BA.
Calculer l’angle en A

BI-PUZZLE

Avec les trois pièces A, B et C on peut former un carré ainsi qu’avec les 4 pièces.
Dessiner les deux carrés ainsi formés.

PLIE ET

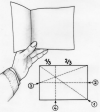
Plier puis déplier successivement la feuille suivant les 4 indications.
Démontrer qu’on obtient ainsi le tiers de la longueur.

Ouverture

Un carré est découpé selon deux droites perpendiculaires en quatre pièces identiques. Ces quatre pièces peuvent être disposées pour réaliser un carré plus grand, créant un carré vide au milieu.
Réaliser un tel découpage de façon que les cinq régions du grand carré soient de même aire. Calculer les valeurs exactes des longueurs des quatre côtés des pièces découpées.

Puzzle magique

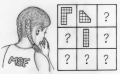
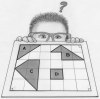
Compléter le puzzle avec les pièces manquantes de sorte que, en assemblant trois pièces d’une même ligne ou d’une même colonne ou d’une même diagonale, on peut à chaque fois former un carré.

Poutre dans l’oeil

l s’agit de repasser sur les segments représentant les poutres du pignon de la maison, sans lever le crayon et sans repasser sur un segment préalablement tracé.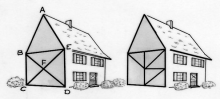

Quels sont les points qui permettent de débuter dans chacune des figures ?
Effectuer le tracé de la deuxième maison.

AU QUART DE TOUR

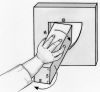
Un carré de 5 cm de côté peut-il effectuer un tour complet dans un quart de disque de rayon 8 cm ?