CM2/6e
Algorithmique et logique
Géométrie
Grandeurs et mesures
Nombres et Calculs
Organisation et gestion de données, fonctions
Au IIIe siècle avant Jésus-Christ, Aristarque de Samos
a donné une assez bonne approximation du
diamètre lunaire à partir de l’observation d’une
éclipse de Lune.
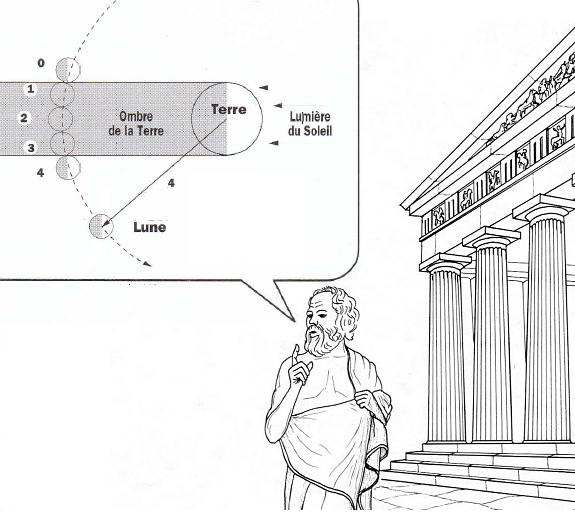
En regardant la Lune quand elle pénètre dans l’ombre de la Terre, il a
mesuré qu’elle parcourt en une heure une distance égale à son diamètre
(voir positions 0-1 de la figure). Elle traverse ensuite cette ombre en deux heures environ (de 1 à 3).
Aristarque en a déduit que le diamètre de la Lune est à peu près égal au
tiers du diamètre terrestre.
En admettant que la Lune décrit à vitesse constante un cercle autour de la Terre en 27 jours, utiliser ces observations pour donner une
estimation de la distance de la Terre à la Lune en nombre de diamètres
terrestres.
Mots-clés : Niveau 3ème, épreuve décembre 1995, exercice 3.
Principaux éléments mathématiques : Distance, vitesse, durée, circonférence, rayon, proportionnalité, astronomie.
Capacités : Reconnaître et traiter des situations relevant de la proportionnalité.
Ce que l’élève doit faire : Lecture attentive, recherche d’information, calcul.
Difficulté : **
(exercice 3)