Un élève du Savant Cosinus lui dit un jour :
"Maître, j’ai trouvé le moyen de construire, sans
rapporteur, un polygone régulier à neuf côtés.
– Un ennéagone régulier ?
– Oui, et voilà comment je procède :
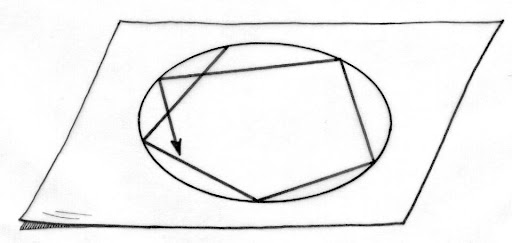
Je trace un cercle de centre 0 et de rayon R.
A partir d un point du cercle, je reporte huit fois au compas une longueur
égale à 9R/7 sur ce cercle.
J’obtiens ainsi les 9 sommets d’un polygone régulier étoilé.
– Tu affirmes donc que 9R/7 est le côté d’un ennéagone étoilé ?...
Permets-moi d’en douter !"
Effectuer la construction de l’élève à partir d’un cercle de rayon 7cm, puis justifier les réserves émises par le Savant Cosinus.
Mots-clés :
Niveau 2de, Epreuve de décembre 1994, exercice 15, spécial seconde.
Principaux éléments mathématiques : Polygone régulier, trigonométrie, angle au centre.
Capacités :Effectuer des tracés avec la règle et le compas, déterminer un angle à l’aide de son sinus, relations trigonométriques dans le triangle rectangle.
Ce que l’élève doit faire : Construire la figure, déterminer l’angle au centre, discuter la qualité de l’approximation.
Difficulté : **.