CM2/6e
Algorithmique et logique
Géométrie
Grandeurs et mesures
Nombres et Calculs
Organisation et gestion de données, fonctions
La trisection d’un angle, c’est son partage en
3 angles égaux ; cela n’est pas possible dans
le cas général avec la règle et le compas.
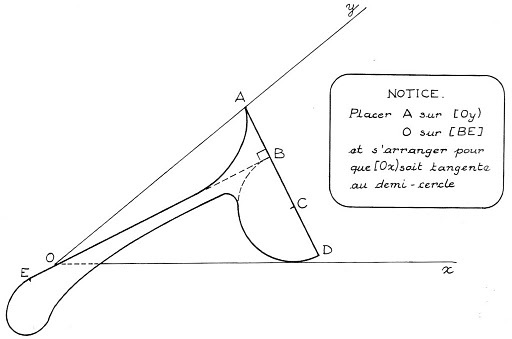
Pourtant, l’instrument ci-dessus, décrit en 1835 dans
"Géométrie appliquée dans l’industrie", permet effectivement cette
opération.
Les points A, B, C et D sont alignés, les segments AB, BC et CD
mesurent tous 3 centimètres. Le segment BD est le diamètre du demi-cercle.
(BE) est perpendiculaire à (AD).
Pour trisecter un angle xÔy, on place l’instrument comme indiqué sur
la figure.
Dessiner un angle xÔy de 50°.
Fabriquer un trisecteur en papier et le coller dans la bonne position.
Démontrer alors l’égalité des angles AÔB, BÔC et CÔx.
Mots-clés :
Niveau 3e, épreuve décembre 1995, exercice 9.
Principaux éléments mathématiques : Trisection d’un angle, droite tangente à un cercle, angles égaux.
Capacités : Analyser une figure, démontrer des égalités d’angles
Ce que l’élève doit faire : Construction, Expliquer, démontrer des égalités d’angles.
Difficulté : **
(exercice 9).
Autres exercices sur ce thème : Trisection d’un angle, mars 1998.