-> Page d'accueil

-> Plan du site

CM2/6^e

THÈMES

Algorithmique
Logique
Pattern
Stratégie

Configurations de l’espace
Configurations du plan
Géométrie analytique

Angles et trigonométrie
Autres grandeurs
Grandeurs composées, changement d’unités
Longueurs, aires et volumes

Écritures littérales
Équations, inéquations
Nombres et numération

Fonction linéaire, fonction affine, proportionnalté
Fonctions
Logique, stratégie, algorithmique
Statistiques et probabilités

Trisection d’un angle

Nicomède découvrit une construction permettant de partager un angle en trois angles égaux.

Voici son procédé : on veut faire la trisection de l’angle xÂy de la figure ci-dessous.

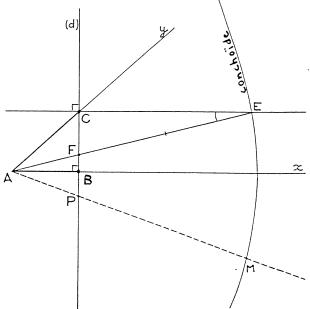
Pour cela on a placé un point C sur le côté [Ay), on a construit la droite (d) passant par C et perpendiculaire au côté [Ax) puis la courbe conchoïde ainsi définie : pour tout point P de (d), la demi-droite [AP) coupe la courbe en M tel que PM = 2AC.

La droite passant par C et perpendiculaire à d coupe la courbe en E.

Démontrer que l’angle xÂE est le tiers de l’angle xÂy. (Il est inutile de construire la conchoïde.)

Mots-clés :
Niveau 3ème , épreuve de mars 1998 , exercice 9.

Principaux éléments mathématiques : Trisection d’un angle, angles égaux, conchoïde de Nicomède

Capacités : uUtiliser les théorèmes de la géométrie plane pour démontrer

Ce que l’élève doit faire :Démontrer des égalités d’angles, rédiger la démonstration.

Difficulté : ***.

Solution

Autres exercices sur ce thème : Trisection, décembre 1995.