CM2/6e
Algorithmique et logique
Géométrie
Grandeurs et mesures
Nombres et Calculs
Organisation et gestion de données, fonctions
Nicole est prévoyante : elle emporte toujours son gobelet pliable dans son sac à main, au cas où il y aurait une occasion de s’en servir.
Le gobelet de Nicole est constitué d’un socle et de cinq pièces coniques en plastique.
Ces cinq éléments peuvent s’emboîter (figure 1) pour former un récipient étanche que l’on peut replier (figure 2).
Figure 1
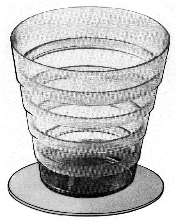
Figure 2
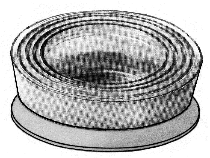
Le schéma ci-dessous représente ce récipient replié.
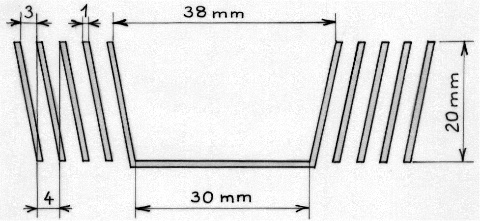
Le plus petit élément a des diamètres intérieurs de 30 et 38 mm. Chaque élément a des rayons de 4 mm de plus que les rayons respectifs de l’élément précédent et une hauteur de 20 mm. Les épaisseurs des parois sont toutes identiques.
Quelle est la hauteur intérieure du gobelet déplié ? Expliquer.
On veut estimer le volume de liquide que peut contenir ce gobelet.
Donner une méthode de calcul et le volume ainsi obtenu.
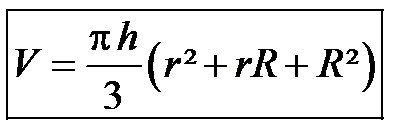
On rappelle la formule du volume d’un tronc de cône :
de rayons r et R et de hauteur h :
Mots-clés : Niveau 2nde , épreuve de décembre 2012 , exercice 13, spécial Secondes.
Principaux éléments mathématiques : Solides, volume, théorème de Thalès.
Capacités : Analyser une figure, mener à bien un calcul instrumenté, évaluer un ordre de grandeur.
Ce que l’élève doit faire : Application de résultats à connaitre, calcul.
Difficulté : ***
(exercice 13).
Autre exercice sur ce thème :
Question de pot, décembre 1996.
cliquer pour agrandir la figure